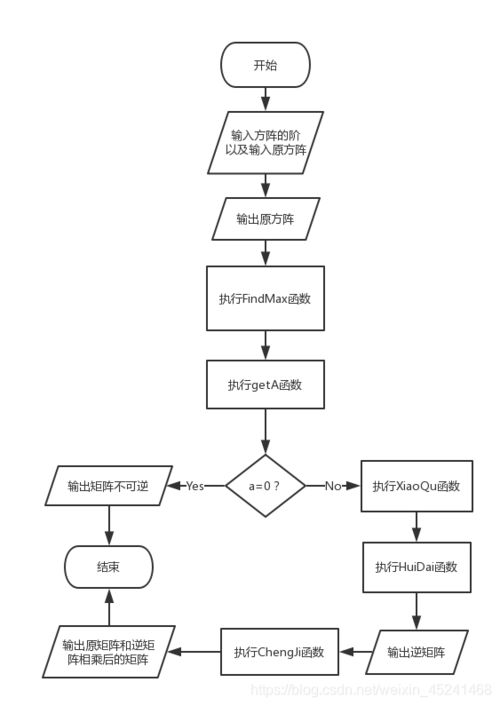
矩阵求逆是线性代数中的核心问题之一，在科学计算、工程应用和数据分析等领域具有广泛的应用。本文将介绍一个基于C语言的n阶矩阵求逆系统的设计与实现，涵盖系统功能、算法原理、关键代码实现以及应用示例。

### 系统功能

本矩阵系统以矩阵求逆为核心，支持以下功能：

1. 输入n阶矩阵：用户可以通过键盘输入或文件读取方式提供矩阵数据。

2. 矩阵求逆：利用高斯-约当消元法或LU分解等算法计算逆矩阵。

3. 结果输出：将逆矩阵以清晰格式显示或保存到文件中。

4. 错误处理：检测输入矩阵是否可逆（如行列式为零时提示错误）。

5. 扩展功能：可选支持矩阵乘法、行列式计算等辅助操作。

### 算法原理

矩阵求逆的常用方法包括高斯-约当消元法和伴随矩阵法。高斯-约当消元法通过行变换将原矩阵转换为单位矩阵，同时对应变换单位矩阵以获得逆矩阵。其步骤包括：

- 构造增广矩阵：[A | I]，其中A为原矩阵，I为单位矩阵。

- 使用行变换将A部分化为单位矩阵，此时I部分变为A的逆矩阵。

- 若在过程中无法将A化为单位矩阵，则矩阵不可逆。

该方法时间复杂度为O(n^3)，适用于大多数可逆矩阵。

### 关键代码实现

以下是使用C语言实现高斯-约当消元法求逆的核心代码片段：

```c

#include

#include

#define MAX_SIZE 10

void matrixInverse(double matrix[][MAX_SIZE], int n) {

double aug[MAX_SIZE][2*MAX_SIZE];

int i, j, k;

// 构造增广矩阵 [A | I]

for (i = 0; i < n; i++) {

for (j = 0; j < n; j++) {

aug[i][j] = matrix[i][j];

aug[i][j+n] = (i == j) ? 1.0 : 0.0;

}

}

// 高斯-约当消元

for (i = 0; i < n; i++) {

if (aug[i][i] == 0.0) {

printf("矩阵不可逆！\n");

return;

}

// 归一化当前行

double pivot = aug[i][i];

for (j = 0; j < 2*n; j++) {

aug[i][j] /= pivot;

}

// 消去其他行

for (k = 0; k < n; k++) {

if (k != i) {

double factor = aug[k][i];

for (j = 0; j < 2*n; j++) {

aug[k][j] -= factor * aug[i][j];

}

}

}

}

// 输出逆矩阵

printf("逆矩阵：\n");

for (i = 0; i < n; i++) {

for (j = n; j < 2*n; j++) {

printf("%.2f\t", aug[i][j]);

}

printf("\n");

}

}

int main() {

double matrix[MAX_SIZE][MAX_SIZE];

int n, i, j;

printf("请输入矩阵阶数n：");

scanf("%d", &n);

printf("请输入矩阵元素：\n");

for (i = 0; i < n; i++) {

for (j = 0; j < n; j++) {

scanf("%lf", &matrix[i][j]);

}

}

matrixInverse(matrix, n);

return 0;

}

```

### 应用与注意事项

本系统适用于教学演示和小规模矩阵计算。在实际应用中，需注意：

- 数值稳定性：对于病态矩阵，高斯消元法可能产生较大误差，可考虑使用SVD分解等更稳定的方法。

- 内存管理：对于大阶矩阵（n>100），需动态分配内存以避免栈溢出。

- 性能优化：可通过并行计算或使用BLAS库提升计算效率。

### 总结

通过C语言实现的n阶矩阵求逆系统，不仅加深了对线性代数算法的理解，还展示了编程解决实际问题的能力。未来可扩展为完整的矩阵运算库，支持更多矩阵操作和优化算法。